我觉得去理解数据结构的时候,需要注意到它其实包含两个层面。一个层面是高一级的,从功能、接口的角度去理解,比如说堆,有什么功用,都有怎样的 API;另一个层面是低一级的,从结构和实现的角度去理解,比如堆的实现,可以用数组实现,也可以用单独的节点对象+指针实现。上面一层相同,但是下面一层不同,功能上可能基本一致,但是性能上针对不同的应用场景就可以天差地别。
图就是另外一个典型例子,无向图也好,有向图也好,这是从功能上说的,但它们各自的实现,或者说基于的 “表示方法” 有多种。我记得在学习数据结构早期,基本上没有比较系统地去比较它们,那今天就把这一课补上。
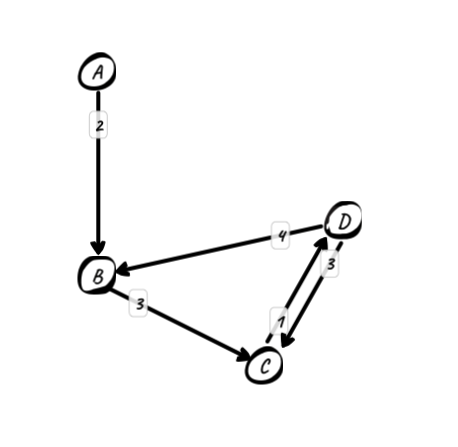
比如上面这个有向图,四个顶点,每条边还带权。我拿带权的有向图来举例,因为我觉得它是相对来说较为复杂的一种图,对于无权和无向图来说,会比它简单一些。
Adjacency Matrix(邻接矩阵)
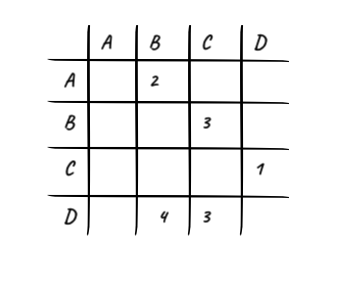
矩阵在编程语言中最常见和自然的表达法就是二维数组,对于许多语言来说,用 null 来表示两个顶点不可直达是很自然的。上面这样表示的边都是带权的,这样的矩阵也被称为距离矩阵(Distance Matrix)。
优点:简单、直观,而且对于任意两点之间的直接关系,可以以 O(1) 的时间复杂度获得。
缺点:在点较多而边较少的时候,成为较稀疏的矩阵,在存储空间上显得浪费。另外,由于这个结构,两个维度都是基于顶点的,对于一些以边主导的操作可能不够友好,比如说,要遍历所有的边,这就必须遍历矩阵的所有节点。
Adjacency List(邻接表)
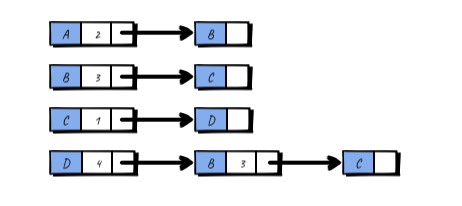
和邻接矩阵相比,二维数组变成了单向链表集合。每个节点表示一个顶点,包含一个指针和相应指针指向顶点所对应的权值。每一个链表的非头元素都表示从头部节点所代表的顶点可以直接指向的其它顶点。不过我们平时更多情况下,会把这些节点都放到一个单独的集合里面去,这个集合可以是 Array, ArrayList, LinkedList 或者 HashSet,于是它就变成了这样:
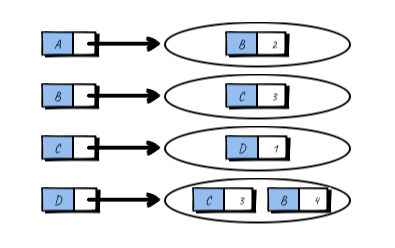
这种方式应该是最常见的,若干个 pair,每个 pair 的 key 都是作为边的起点的顶点,value 则是终点和边的权值的集合。
还有两种用链表来代替二维数组的变体。一种叫做 Orthogonal Linked List(十字链表),对于从起点找终点和从终点找起点都很方便,它本质上也是矩阵压缩方式的一种;另一种叫做邻接多重表,它把边独立成一种 “边节点”,这样在无向图中,就不需要把边(顶点之间的映射关联关系)存储两次。它们相对来说都更为复杂,用得也没有上面两种多。
优点:无论哪一种,和邻接表比起来,在面临稀疏矩阵的时候,都要更加节约空间。并且,作为链表 vs 数组的优势,在添加删除节点的时候都要更加容易(不用 shift 大量元素)。
缺点:相较于邻接表来说,结构上要略微复杂一些,操作上的开销也往往更大一些。
Incidence Matrix(关联矩阵)
Incidence Maxtrix 也有翻译成输入矩阵,我觉得也很形象,但是有的材料把它和前面的邻接矩阵完全归为一类我觉得就不妥了。这里的 “incidence” 需要这样理解:如果一个顶点被一条边所连接,那么这个顶点对于这条边来说就是 “incident” 的。所以这个关联矩阵一定是顶点和边的对应关系矩阵。
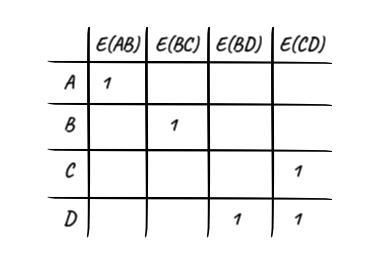
依然是二维数组实现的矩阵,行表示顶点,列表示边。边的具体信息,例如它所具有的权值(不同向权值不同)存储在边这个数据结构内部,而这个矩阵只表示顶点和边之间的关联关系。并且,二维数组依然可以有效地表示出边的方向性。
此外,矩阵中的数值可以进一步强化。比如,上面的数字 1 表示以对应的顶点为起点,是否存在该对应的边;还可以引入一个值-1,用以表示以对应的顶点为终点,是否存在该对应的边。
优点:和邻接矩阵比起来,对于需要根据一条单独的边来获取它和点之间的关联信息,就可以从关联矩阵中直接获取。再有一个,如果两个点之间有同方向的一条以上的边,用关联矩阵相对来说就比较容易表示。
缺点:和邻接矩阵类似,较稀疏的矩阵会导致较大的空间浪费。如果需要点之间的关系,它就不如邻接矩阵高效。
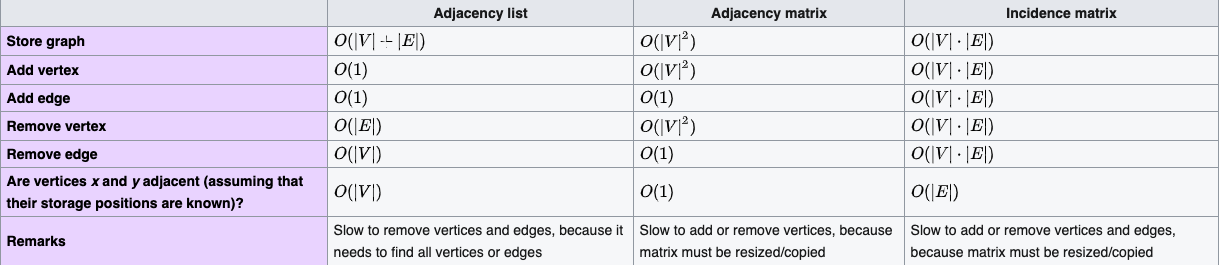
最后,对于上面三者大体上时间复杂度的总结,可参加下面这张表(来自维基百科):
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》