排序算法一览（上）：交换类、选择类和插入类排序

• 交换类排序 – 冒泡排序 鸡尾酒排序 奇偶排序 梳子排序 侏儒排序 快速排序 臭皮匠排序 Bogo 排序
• 选择类排序 – 选择排序 堆排序 Smooth 排序 笛卡尔树排序 锦标赛排序 圈排序
• 插入类排序 – 插入排序 希尔排序 二叉查找树排序 图书馆排序 耐心排序
• 归并类排序 – 归并排序 梯级归并排序 振荡归并排序 多相归并排序 Strand 排序
• 分布类排序 – 美国旗帜排序 珠排序 桶排序 计数排序 鸽巢排序 相邻图排序 基数排序
• 混合类排序 – Tim 排序 内省排序 Spread 排序 UnShuffle 排序 J 排序

本文中出现的排序信息大部分收集自维基百科，以上的排序列表源自此页面（链接），列表中蓝色标注的排序方式为算法课本中介绍过的，几种最常用的排序方式。

交换类排序

冒泡排序（Bubble Sort）

最原始的交换类排序方式。走访要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

 i∈[0,N-1)                //循环 N-1 遍
   j∈[0,N-1-i)            //每遍循环要处理的无序部分
     swap(j,j+1)          //两两排序（升序/降序）

鸡尾酒排序（Cocktail Sort）

也就是定向冒泡排序, 搅拌排序, 是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低，而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能，原因是冒泡排序只从一个方向进行比对 (由低到高)，每次循环只移动一个项目。

for (int i = 0; i < a.length / 2; i++) {
  for (int j = i; 1 + j < a.length - i; j++)
    if (a[j] > a[1 + j])
      Arr.swap(a, j, 1 + j);
  for (int j = a.length - i - 1; j > i; j--)
    if (a[j - 1] > a[j])
      Arr.swap(a, j - 1, j);
}

奇偶排序（Odd-even Sort）

也叫奇偶换位排序，是一种相对简单的排序算法，原始的奇偶排序很低效，最初发明用于有本地互连的并行计算，在并行计算排序中，每个处理器对应处理一个值，并仅有与左右邻居的本地互连。这是与冒泡排序特点类似的一种比较排序。通过比较数组中相邻的（奇-偶）位置数字对，如果该奇偶对是错误的顺序（第一个大于第二个），则交换。下一步重复该操作，但针对所有的（偶-奇）位置数字对。如此交替进行下去。

var sorted = false;
while(!sorted){
  sorted=true;
  for(var i = 1; i < list.length-1; i += 2){
    if(a[i] > a[i+1]){
      swap(a, i, i+1);
      sorted = false;
    }
  } //for
  for(var i = 0; i < list.length-1; i += 2){
    if(a[i] > a[i+1]){
      swap(a, i, i+1);
        sorted = false;
    }
  } //for
}

梳子排序（Comb Sort）

梳子排序是改良自冒泡排序和快速排序的不稳定排序算法，其要旨在于消除乌龟（在阵列尾部的小数值，这些数值是造成泡沫排序缓慢的主因；相对地，兔子指的是在阵列前端的大数值，它不影响冒泡排序的性能）。在冒泡排序中，只比较阵列中相邻的二项，即比较的二项的间距是 1，梳子排序提出此间距其实可大于 1，改自插入排序的希尔排序同样提出相同观点。梳子排序中，开始时的间距设定为阵列长度，并在循环中以固定比率递减，通常递减率设定为 1.3。在一次循环中，梳子排序如同冒泡排序一样把阵列从首到尾扫描一次，比较及交换两项，不同的是两项的间距不固定于 1。如果间距递减至 1，梳子排序假定输入阵列大致排序好，并以泡沫排序作最后检查及修正。

int gap = input.length;
boolean swapped = true;
while (gap > 1 || swapped) {
    if (gap > 1) {
        gap = (int) (gap / 1.3);
    }
    int i = 0;
    swapped = false;
    while (i + gap < input.length) {
        if (input[i].compareTo(input[i + gap]) > 0) {
            E t = input[i];
            input[i] = input[i + gap];
            input[i + gap] = t;
            swapped = true;
        }
        i++;
    }
}

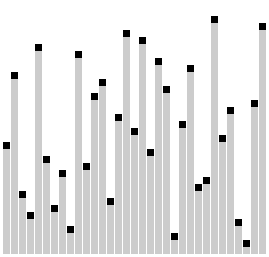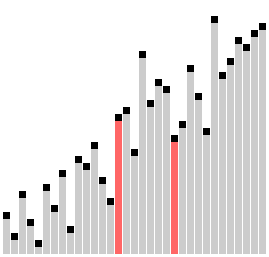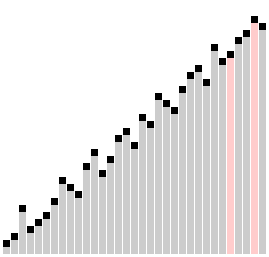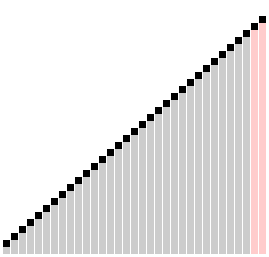
侏儒排序（Gnome Sort）

也叫地精排序、Stupid Sort，号称写出来最简单的排序代码，它很像冒泡，也是通过一系列的元素交换完成的。这个算法你初看起来只有一层循环，但是实际上它的游标却并不总是往前进的，有时需要后退，所以总的时间复杂度并不小。这个算法总是能够找到第一组大小顺序错误的毗邻元素，然后交换它们。但是交换这两个元素的时候，又可能会带来新的顺序错误的毗邻元素对，所以在交换元素之后需要重新检查影响到的毗邻元素。

procedure gnomeSort(a[])
  pos := 1
  while pos < length(a)
    if (a[pos] >= a[pos-1]) //毗邻元素顺序正确，前进
      pos := pos + 1
    else
      swap a[pos] and a[pos-1]
      if (pos > 1) //交换元素可能会带来新的毗邻元素顺序错误
        pos := pos - 1 //所以游标回退
      end if
    end if
  end while
end procedure

快速排序（Quick Sort）

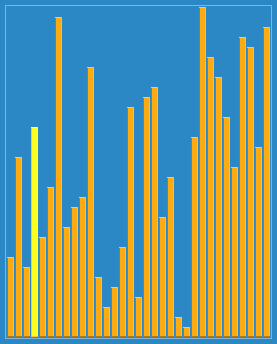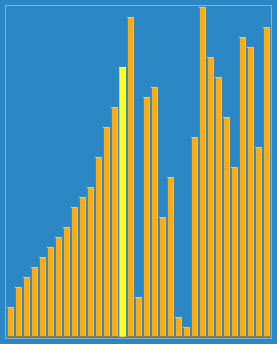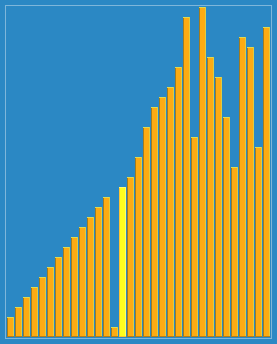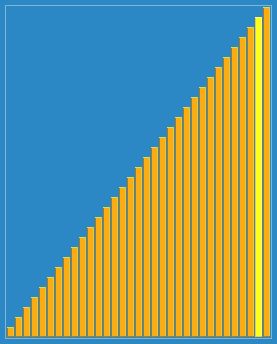
前面的算法平均时间复杂度都在Ο(n²) 阶，而快速排序在平均状况下，排序 n 个项目只需要Ο(n*logⁿ) 次比较，在最坏状况下依然需要Ο(n²) 次比较，它比前面介绍的排序都要快。事实上，快速排序通常明显比其他Ο(n*logⁿ) 算法更快。步骤为：

• 从数列中挑出一个元素，称为 “ 基准”（pivot）。
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

function partition(a, left, right, pivotIndex)
  pivotValue := a[pivotIndex]
  swap(a[pivotIndex], a[right]) // 把 pivot 移到結尾
  storeIndex := left
  for i from left to right-1
    if a[i] < pivotValue
      swap(a[storeIndex], a[i])
      storeIndex := storeIndex + 1
  swap(a[right], a[storeIndex]) // 把 pivot 移到它最後的地方
  return storeIndex

procedure quicksort(a, left, right)
  if right > left
    select a pivot value a[pivotIndex]
    pivotNewIndex := partition(a, left, right, pivotIndex)
    quicksort(a, left, pivotNewIndex-1)
    quicksort(a, pivotNewIndex+1, right)

臭皮匠排序（Stooge Sort）

Stooge 排序是一种低效的递归排序算法，甚至慢于冒泡排序。实现：

• 如果最后一个值小于第一个值，则交换它们
• 如果当前子集元素数量大于等于 3：
  • 使用臭皮匠排序前 2/3 的元素
  • 使用臭皮匠排序后 2/3 的元素
  • 再次使用臭皮匠排序前 2/3 的元素

algorithm stoogesort(array L, i = 0, j = length(L)-1)
  if L[j] < L[i] then
    L[i] ↔ L[j]
  if (j - i + 1) >= 3 then
    t = (j - i + 1) / 3
    stoogesort(L, i  , j-t)
    stoogesort(L, i+t, j  )
    stoogesort(L, i  , j-t)
  return L

Bogo 排序（Bogo Sort）

Bogo 排序其实就是大名鼎鼎的猴子排序（“猴子排序” 的名字出自 “无限猴子定理”：让一只猴子在打字机上随机地按键，当按键时间达到无穷时，几乎必然能够打出任何给定的文字，比如莎士比亚的全套著作——只要时间足够。），是个既不实用又原始的排序算法，其原理非常简单，将一堆卡片抛起，落在桌上后检查卡片是否已整齐排列好，若非就再抛一次。所以，它的最坏时间复杂度是正无穷，平均时间复杂度也达到了 n*n!（因为抛起来出现任意一组解的概率是 A(n,1)，即 1/(n!)，那么期望抛 n! 次才能遇到一次正确的解，每次检查解是否正确的需要线性的时间复杂度，于是二者相乘得到 n*n!）。

Random random = new Random();

public void bogoSort(int[] n) {
  while(!inOrder(n))shuffle(n);
}

// 洗牌，挨个遍历，每个元素都和位置小于等于它的随机元素交换
public void shuffle(int[] n) {
  for (int i = 0; i < n.length; i++) {
    int swapPosition = random.nextInt(i + 1);
    int temp = n[i];
    n[i] = n[swapPosition];
    n[swapPosition] = temp;
  }
}

public boolean inOrder(int[] n) {
  for (int i = 0; i < n.length-1; i++) {
    if (n[i] > n[i+1]) return false;
  }
  return true;
}

选择类排序

选择排序（Selection Sort）

选择排序的工作原理如下。首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 n 个元素的表进行排序总共进行至多 n-1 次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。如果移动元素的代价非常大，使用选择排序可以保证最少次数的数据移动。

void selection_sort(int *a, int len)
{
  register int i, j, min, t;
  for(i = 0; i < len - 1; i ++)
  {
    min = i;
    //查找最小值
    for(j = i + 1; j < len; j ++)
      if(a[min] > a[j])
        min = j;
    //交换
    if(min != i)
    {
      t = a[min];
      a[min] = a[i];
      a[i] = t;
    }
  }
}

堆排序（Heap Sort）

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。如果堆通过一维数组来实现，在起始数组为 0 的情形中：

• 父节点 i 的左子节点在位置 (2*i+1);
• 父节点 i 的右子节点在位置 (2*i+2);
• 子节点 i 的父节点在位置 floor((i-1)/2);

对于堆来说，由于满节点的第 k 层（k≥0），该层的节点数目正好是 2^k，所以上述结论不难得出。在堆的数据结构中，堆中的最大值总是位于根节点。堆中定义以下几种操作：

• 最大堆调整（Max_Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
• 创建最大堆（Build_Max_Heap）：将堆所有数据重新排序
• 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

其实，整个过程是，上述三条中的最后一条 “堆排序（HeapSort）” 是入口，最初需要创建最大堆（Build_Max_Heap）一次，之后循环中反复执行如下操作：拿掉堆顶的最大值，转而以堆尾部的一个较小的值替换，此时这个堆已经不再符合堆了，于是执行最大堆调整（Max_Heapify）使之成为堆，所以堆排序被归在了 “选择类排序” 中，由此也可见，堆排序的最差、最好，乃至平均复杂度都在Ο(n*logⁿ) 级别。这张图（出处在此）可以非常清晰地帮助理解最大堆调整的整个过程：

void Max_Heapify(int A[], int i, int heap_size)
{
  int l = left(i);
  int r = right(i);
  int largest;
  int temp;
  if(l < heap_size && A[l] > A[i])
  {
    largest = l;
  }
  else
  {
    largest = i;
  }
  if(r < heap_size && A[r] > A[largest])
  {
    largest = r;
  }
  if(largest != i)
  {
    temp = A[i];
    A[i] = A[largest];
    A[largest] = temp;
    Max_Heapify(A, largest, heap_size);
  }
}
 
void Build_Max_Heap(int A[]，int heap_size)
{
  for(int i = (heap_size-2)/2; i >= 0; i--)
  {
    Max_Heapify(A, i, heap_size);
  }
}
 
void HeapSort(int A[], int heap_size)
{
  Build_Max_Heap(A, heap_size);
  int temp;
  for(int i = heap_size - 1; i >= 0; i--)
  {
    temp = A[0];
    A[0] = A[i];
    A[i] = temp;
    Max_Heapify(A, 0, i);
  }
  print(A, heap_size);
}

平滑排序（Smooth Sort）

平滑排序是堆排序的一个变种，源于大名鼎鼎的 Dijkstra。堆排序主要的问题在于即便是在最好的情况下复杂度还是Ο(n*logⁿ) 的，平滑排序可以把它优化成为 O(n)。和堆排序一样，构建一个最大堆（或者最小堆），然后不断执行从堆顶拿掉元素，再重新调整堆的过程；不一样的地方在于，平滑排序并不使用最常见的二叉堆（Binary Heap），取而代之的是一些基于 Leonardo 数的堆，这些堆的特点是大小都是 Leonardo 数，它们组成一个优先级队列，这种优先队列在取出最大元素后剩余元素可以就地调整成优先队列，所以平滑排序不用像 Heap Sort 那样反向地构建堆，这就是它为什么在好的情况下时间复杂度可以达到 O(n) 的原因。Leonardo 数的定义如下（很像斐波那契数列）：

把输入变成一系列的堆很简单，数组最左边的节点要创建尽可能大的堆，剩下的再来划分：

• 任意数组长度都可以划分成若干 L(x)。
• 不存在两个堆有相同的大小，因此这一系列堆会是严格递减排列的。
• 不存在两个相邻的堆的大小由不相邻的 Leonardo 数组成，除非是这一系列堆中最后的两个。

平滑排序的时间复杂度理论值非常好，但由于它所用的优先队列是基于一种不平衡的结构，乘积因子很大，所以该算法的实际效率并不是很好。算法略显复杂，在维基百科和 paroid 掘趣上有比较详细的说明。

笛卡尔树排序（Cartesian Tree Sort）

无相同元素的数列构造出的笛卡尔树具有下列性质：

• 结点一一对应于数列元素。即数列中的每个元素都对应于树中某个唯一结点，树结点也对应于数列中的某个唯一元素
• 中序遍历（in-order traverse）笛卡尔树即可得到原数列。即任意树结点的左子树结点所对应的数列元素下标比该结点所对应元素的下标小，右子树结点所对应数列元素下标比该结点所对应元素下标大。
• 树结构存在堆序性质，即任意树结点所对应数值大／小于其左、右子树内任意结点对应数值

根据堆序性质，笛卡尔树根结点为数列中的最大／小值，树本身也可以通过这一性质递归地定义：根结点为序列的最大／小值，左、右子树则对应于左右两个子序列，其结点同样为两个子序列的最大/小值。因此，上述三条性质唯一地定义了笛卡尔树。若数列中存在重复值，则可用其它排序原则为数列中相同元素排定序列，例如以下标较小的数为较小，便能为含重复值的数列构造笛卡尔树。

排序方式在这里（链接）有详细说明。

锦标赛排序（Tournament Sort）

锦标赛排序也称为树形选择排序（Tree Selection Sort），这棵树是胜者树，它其实是堆排序的前身，是一种按照锦标赛的思想进行选择排序的方法。为何叫做 “锦标赛排序”？其实，锦标赛指的是这样一种比赛方法，有很多参赛者需要进行两两之间的循环比赛，并且每场比赛的胜者会进入下一轮，如此进行知道最后一场比赛决定谁是最终胜者。所以锦标赛本身可以确定 “最好” 的那个参赛者，但是最后一场比赛（决赛）中被击败的那位，却未必是 “次好” 的参赛者。

具体排序方法也很简单，首先对 n 个记录进行两两比较，然后优胜者之间再进行两两比较，如此重复，直至选出最小关键字的记录为止。这个过程可以用一棵有 n 个叶子结点的完全二叉树表示。根节点中的关键字即为叶子结点中的最小关键字。在输出最小关键字之后，根据关系的可传递性，欲选出次小关键字， 仅需将叶子结点中的最小关键字改为 “最大值”，如∞，然后从该叶子结点开始，和其左（右）兄弟的关键字进行比较，修改从叶子结点到根的路径上各结点的关键 字，则根结点的关键字即为次小关键字。 直接选择排序之所以不够高效就是因为没有把前一趟比较的结果保留下来，每次都有很多重复的比较。锦标赛排序克服了这一缺点，它利用一棵满二叉树来记录下之前比较的结果，减少了一些冗余的比较（首先需要花费出示的 O(n) 时间构建锦标赛结构，接下去每次只需要花费 O(logⁿ) 选择元素）；但是它也有自己的缺点：辅助存储空间较多、最大值进行多余的比较。

在 Class Xman 的博客上记录了非常清晰的锦标赛排序的具体过程：

在第一次锦标赛中找到了最小的元素（也是建立树的过程），之后的一次比较需要把最小元素置为最大（如∞），然后重新进行红色链路上元素的锦标赛比较即可（不需要整棵树全部做一遍比较了，因为只有红色链路上的元素会被影响到），依此类推。

圈排序（Cycle Sort）

圈排序又叫循环排序，是不稳定的原地排序算法。选择排序本来已经让写元素的次数变得很少了，但是圈排序可以让它更少：试想一下这种情况，位置 1 的元素应该放当前位置 3 的元素，选择排序把当前位置 3 的元素和位置 1 的元素互换——那么原本位置 3 的元素，直接就到达了最后它应该在的位置；但是原本位置 1 的元素呢，却有可能会被再换位置，也就是说，选择排序依然可能存在着某元素被换了不止一次地方。圈排序真正使得任一元素要么不动，要动也最多动一次。圈排序最好和最坏的时间复杂度都是 O(n²)，但是因为最小的写入次数，对于在写入非常慢的介质中排序来说，会有它的价值（例如在某些 Flash 闪存中）。

假使原来的数列 a 是 [3,0,2,1,4]，那么如果从小到大排列的话：

• a[0] 应该是 0，也就是当前的 a[1]，那么当前的 a[1] 应该放什么呢？
• 应该放 1，也就是当前的 a[3]，那么当前的 a[3] 应该放什么呢？
• 应该放 3，也就是当前的 a[0]——可以看到 a[0]、a[1] 和 a[3] 就构成了一个 “圈”；
• a[2] 呢？位置正确，不需要移动；
• a[4] 呢？位置正确，不需要移动。

也就是说，现在只需要写入三次，就完成了整个数列的排序，排好序的数列如下图：

插入类排序

插入排序 (Insertion Sort)

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用原地排序（即只需用到 O(1) 的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。整个过程的时间复杂度在最坏和平均坏的情况下都是 O(n²)，在最好的情况下是 O(n)。

void insertion_sort(int array[], int first, int last)
{
  int i,j;
  int temp;
  for (i = first+1; i<=last;i++)
  {
    temp = array[i];
    j=i-1;
    while((j>=first) && (array[j] > temp))
    {
      array[j+1] = array[j];
      j--;
    }
    array[j+1] = temp;
  }
}

希尔排序（Shell Sort）

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

• 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率；
• 但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位。

原始的算法实现在最坏的情况下需要进行 O(n²) 的比较和交换。希尔排序可以使得性能提升至 O(n*log²n)。这比最好的比较算法的 O(n*logⁿ) 要差一些。希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为 O(n²) 的排序（冒泡排序或插入排序），可能会进行 n 次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。

选择不同的步长序列是影响希尔排序速度的主要因素：

已知的最好步长序列是由 Sedgewick 提出的 (1, 5, 19, 41, 109,…)，该序列的项来自 9*4ⁱ-9*2ⁱ+1 和 4ⁱ-3*2ⁱ+1 这两个算式。这项研究也表明 “比较在希尔排序中是最主要的操作，而不是交换”。用这样步长序列的希尔排序比插入排序和堆排序都要快，甚至在小数组中比快速排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

const int n = 5;
int i, j, temp;
int gap = 0;
int a[] = {5, 4, 3, 2, 1};
while (gap<=n)
{
  gap = gap * 3 + 1;
}
while (gap > 0)
{
  for ( i = gap; i < n; i++ )
  {
    j = i - gap;
    temp = a[i];
    while (( j >= 0 ) && ( a[j] > temp ))
    {
      a[j + gap] = a[j];
      j = j - gap;
    }
    a[j + gap] = temp;
  }
  gap = ( gap - 1 ) / 3;
}

二叉查找树排序（Binary Search Tree Sort）

对一组数值，构造一棵二叉查找树的同时也把这组数值实现了排序。其最差时间复杂度为 O(n²)。该组数值如果已经是自小至大有序，则构造出来的二叉查找树的所有节点都没有左子树。自平衡二叉查找树可以克服上述缺点，时间复杂度为 O(nlogⁿ)。但是，树排序的问题是 CPU Cache 性能差，特别是当节点是动态内存分配时。而堆排序的 CPU Cache 性能好。另一方面，树排序是最优的增量排序（incremental sorting）算法，保持一个数值序列的有序性。

def build_binary_tree(values):
  tree = None
  for v in values:
    tree = binary_tree_insert(tree, v)
  return tree

def get_inorder_traversal(root):
  '''
  Returns a list containing all the values in the tree, starting at *root*.
  Traverses the tree in-order(leftChild, root, rightChild).
  '''
  result = []
  traverse_binary_tree(root, lambda element: result.append(element))
  return result

最坏情况下，当先后插入的关键字有序时，构成的二叉查找树蜕变为单支树，树的深度为 n，其平均查找长度为 (n+1)/2（和顺序查找相同），最好的情况是二叉查找树的形态和折半查找的判定树相同，其平均查找长度和 log₂n 成正比。

图书馆排序（Library Sort）

图书馆排序是基于插入排序改进了的版本，它在元素之间添加了一些空位置，以便在插入排序过程中向后依次移动元素的时候可以减少移动的次数。假使有一个图书馆，书籍都是按照书名的字母序排好的，从左侧的 A 到右侧的 Z，中间没有间隔。假设图书管理员需要新放入一本书名以 B 开头的书，那他先要找到那个位置，然后把那个位置开始一直往右的书都往后移动，给这本新书腾出位置，这就是普通插入排序。现在，如果他预先在这一系列书之间预留一些空位，那么他在需要插入这本新书的时候，他只需要移动很少的书就可以做到了。

图书馆排序的最坏时间复杂度是 O(n²)，即要插入的地方都在同一处，留空位的策略根本没用；最好的时间复杂度是线性的，O(n)；平均时间复杂度是 O(n*logⁿ)。它的缺点在于额外的空间占用，还有一个缺点来自于插入排序，存在大量的交换操作，如果这样的交换导致的写操作开销大的话会成为一个问题（虽然在插入步骤中开销已经好过普通的插入排序，但是在 rebalancing 步骤中增加了额外的开销）。

算法步骤说明：

假设我们有一个 n 元数组，然后我们选定了元素间需要预留的空当大小，这样最后这个数组大小是 (1 + ε)n。我们需要使用二分查找方式找到元素需要插入的位置，接着往数组里插入元素时，因为元素之间有空当，我们需要移动的元素数量会少过普通插入排序，在插入步骤完成后，我们需要执行重平衡（re-balancing，即给元素之间再补充上需要的空当）：

• 二分查找步骤，线性时间；
• 插入步骤，插入元素，如果没有插入空当，需要向后移动元素，直到空当出现；
• 重平衡，给元素之间插入需要的空当，这也应该是线性时间的，因为总共有 O(logⁿ) 轮，所以总的时间复杂度是 O(n*logⁿ)。

耐心排序（Patience Sort）

耐心排序源于一个 “solitaire” 纸牌（卡片）游戏，这个游戏可以很容易找到给定数组内最长递增子串的长度。它的规则是，现在有一组以某种顺序排好的卡片，每张卡片都写有一个数字，任意两张都不相同，我一张一张把它们取出来：

• 桌上有一个区域从左自右放卡片堆（pile），第一张卡片作为第一堆放在最左边。
• 之后每来一张卡片，就判断这张卡片和从左到右的卡片堆的堆顶依次比较，如果小于该卡片，就把这张新卡片放在这个堆的上面，使之成为新的堆顶；否则，向右移动，寻找新的堆，直到没有堆了，就自己建立一个新的堆。
• 等到卡片全部排完了，堆的数量就是给定数组最长递增子串的长度。

比如我有卡片 4、2、6、1、8、3、7，一组括号表示一个堆，括号内最左边的数是堆顶：

(4) => (2,4) => (2,4) (6) => (1,2,4) (6) => (1,2,4) (6) (8) => (1,2,4) (3,6) (8) => (1,2,4) (3,6) (7,8)

最长递增子串的长度就是 3。卡片游戏结束了，但是，我们是要排序，所以还没有结束，我们还需要做的是，对这些堆，反复去取最小的堆顶：

• 第一次，取堆顶 1，堆变成了 (2,4) (3,6) (7,8)；
• 第二次，取堆顶 2，堆变成了 (4) (3,6) (7,8)；
• 第三次，取堆顶 3，堆变成了 (4) (6) (7,8)；
• ……

另外，在实际排序的过程中，每个堆可以使用一个有效的优先级队列（比如用一个二叉堆实现）来优化时间复杂度，总的来看，这个排序算法的时间复杂度是 O(n*logⁿ)。

下半部分请参见 《排序算法一览（下）：归并类、分布类和混合类排序》。

文章未经特殊标明皆为本人原创，未经许可不得用于任何商业用途，转载请保持完整性并注明来源链接 《四火的唠叨》