有时候忽然上下班路上,会去思考一些司空见惯的问题,有一些问题随着思考深入,发现还挺有意思的,就记录在这里。问题之间关联关系不大,有点散。
倒时差的问题
西雅图夏令时和北京时间的时差是 15 个小时,有一个简单的换算方式,就是把当前西雅图时间昼夜颠倒一下(加 12 小时),再加 3 个小时,就得到北京时间了。举例来说,现在是 8 月 16 日晚上的 9 点 37 分,昼夜颠倒一下,就是 8 月 17 日的上午的 9 点 37 分,再加 3 小时,就是 8 月 17 日中午的 12 点 37 分,这就是北京时间。
这几年跑了几次北京和西雅图以后,发现一个规律,就是从北京来到西雅图倒时差非常困难,而从西雅图回到北京倒时差就相对容易得多。我曾经以为是自己心理作用,后来发现同事们也有这样的感受。初想想这很奇怪啊,按理说从 A 到 B 的时差是 c 的话,那么从 B 到 A 的时差就是-c,既然时差的绝对值一样,那为什么二者倒时差的痛苦程度差那么多?
于是我听到各种版本的解释,比如说,一种解释是,从西雅图到北京,到达的时候是晚上,黑夜里面一觉睡过去就容易很多;从北京回西雅图,到达的时候是早上,白天要挺着不睡觉很困难。后来想想,似乎颇为牵强。接着再往下想的时候,忽然想到,其实这两者难度差异的本质原因,是因为人短时间内倒时差靠的是熬夜,而非提早入睡,因此倒时差的时间方向,是单向的。
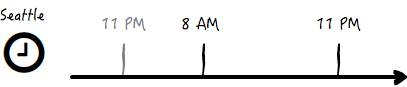
比如说,我习惯每天晚上 11 点入睡,那么当我从北京来到西雅图的时候,北京的晚上 11 点是西雅图的早上 8 点 。在短时间内倒时差的方法,就是硬扛着不睡觉,一旦白天睡觉了,倒时差的效果就非常差,有点前功尽弃的意思。如果要坚持到西雅图的晚上 11 点,就意味着需要额外坚持 15 个小时不睡觉。见下图:
而从西雅图到北京,西雅图的晚上 11 点是北京的下午 2 点,那么依然要坚持到晚上 11 点才睡觉的话,只需要额外坚持 9 个小时,这足足比前面一种情况少了 2/5。见下图:
对,这就是最本质的原因。而实际上由于我们可以在疲乏的时候提早睡觉,就是说睡觉的时间点在倒时差的时候会比晚上 11 点提前一下,那么上述的比例差别会更大。比方说,如果倒时差的时候我们提前到晚上 8 点睡觉,那么从北京到西雅图,需要额外坚持 12 小时不睡觉,而从西雅图到北京,则要坚持 6 小时不睡觉,这时后者就被前者足足少了 1/2 的时间。
如果人短时间内倒时差可以是双向的,那情况就不同了。从北京出发,到西雅图的时间是早上 8 点,但如果我们能在飞机上提早睡觉,往回找 9 个小时,则提早到了西雅图的晚上 11 点睡觉,这 9 个小时的提前量,和从西雅图飞回北京这种情况下,需要晚睡 9 小时的绝对值是一样的。换言之,如果倒时差的时间方向可以是双向的话,从 A 到 B 和从 B 到 A 的时差绝对值是一样的,倒时差的难度也是一样的。
只可惜人并非这样构造的生物,困了可以挺着,不困的时候要提前入睡真是比登天还难,于是我们短时间内倒时差的方法,都是得牺牲睡眠,靠晚睡的方式逐步把生物钟掰过来。如果时间足够,那么可以逐步调整时差,就可以采用 “向回调整” 的方式,即提早睡觉的方式,比如每天提早半小时,逐步逐步把时差调整过来,但那又是另一回事了。
Mealpal 地图设计的问题
Mealpal 是一款订餐软件,上面有这样一个功能,在地图上可以选定任意大小的一个矩形范围,Mealpal 需要列出这个矩形范围内所有 Mealpal 支持的饭馆,每个饭馆的位置可以简单考虑为经度和纬度的而为坐标。
于是我就忽然想,这个功能该怎样实现呢?这个背后的数据结构是怎样的呢?第一反应是想,如果可以经纬度分开处理,是不是就可以搞定?比方说,只考虑经度的话,所有饭馆按照从小到大的顺序排好,这样的话,当给定矩形范围的时候,就可以快速找得到这个范围内所有经度满足条件的饭馆,在不做额外优化的情况下,这个复杂度是 log(n)。
可是,当再考虑纬度的时候,就傻眼了,假如有 m 家满足经度条件的饭馆,接下去需要挨个检查这 m 家饭馆,找出它们中满足纬度条件的来,因此总的时间复杂度是 m*log(n),在 m 比较大的时候,这个计算是很慢的,看起来这个方法不是很好。
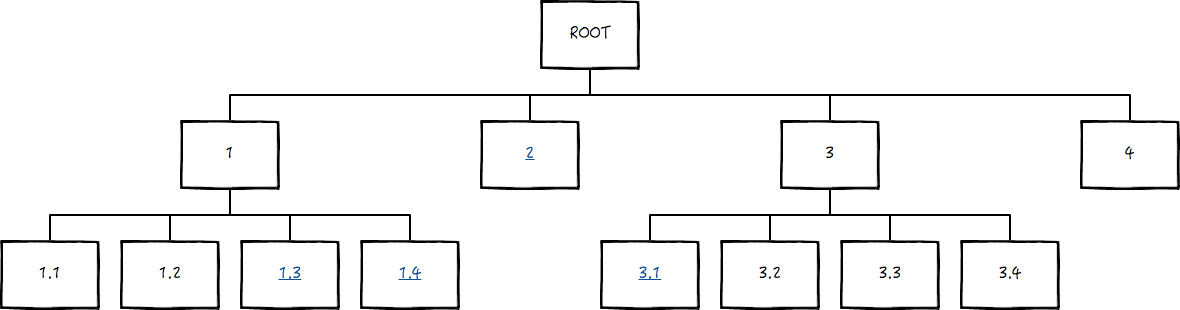
因此需要一种更高效的办法。经度和纬度的大致思路可以,但是在框选饭馆的时候,不能经度和纬度分别框选,而应结合起来框选,并且把复杂度依然控制在 log(n) 的级别。既然范围是一个矩形,那么在常见的数据结构中,四叉树就是可以天然地将矩形递归分解的方式。
上图是个简单示例,每一个矩形都被分解成等大小的四个区域,带有链接(下划线)的数字表示该区域属于框选范围,需要考察其下的饭馆。这种方式有一个好处,就是如果这个行为比较复杂,整个过程是可以分别递归到每棵子树分别求解的,每个子树的求解过程是可以并行化的。
还有一些更具备实际可行性的方法,比如 Geohash,大致思路是把一个经度和纬度的二维坐标用一个一维的字符串来表示。具体实现上,比如一种常见的办法就是把经度和纬度用一个长位数的数来表示,比如:
- 经度:101010……
- 纬度:100110……
接着把二者从左到右挨个位拼接,黑色字符来自经度,蓝色字符来自纬度:
110010011100……
这种方式下,从结果的左边最高位开始,取任意长度截断所得到的前缀,可以用来匹配距离目标位置一定距离范围的所有饭馆。前缀长度越长,这个匹配精度越高,匹配到的饭馆数量也越少。通过这种方式,区域不断通过前缀的方式被细分,相当于给每个子区域一个标记号码。
在 geohash.org 的网站上,可以通过给出经纬度坐标,在地图上找到这个实际位置。
本质上,类似这种二维到一维的降维方式,都属于空间填充曲线,比如说最有名的这种希尔伯特曲线,Google 的 s2geometry 用到。
开机时 Windows 更新等待的问题
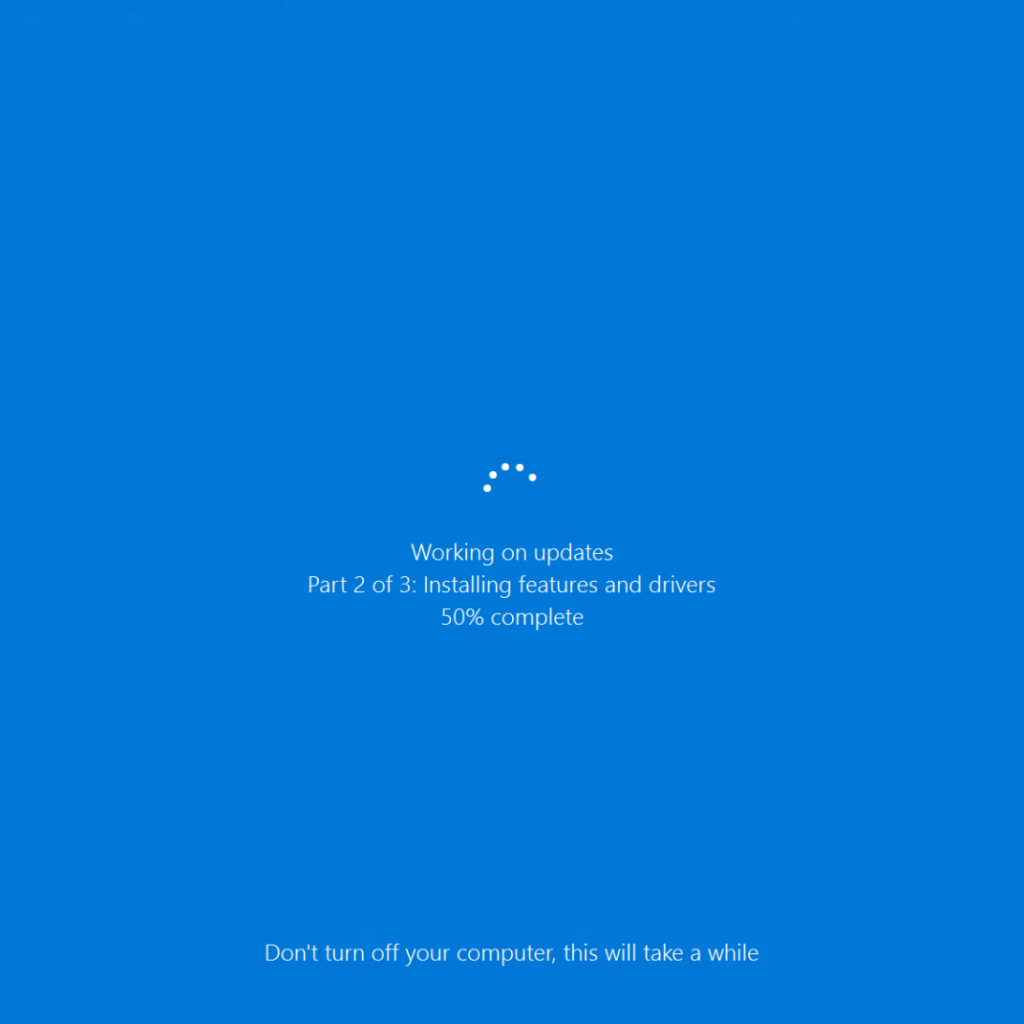
家里有一台 Windows 10 的电脑,主要是存放资料、看球和打游戏用(平时学习工作都是 Mac),一般情况下,只休眠,不关机。一个原因是休眠唤醒的速度比较快,另一个原因是 Windows 奇恶无比的开机更新。比方说,我打开电脑,想急着用呢,却看到这样的画面:
这有时候可真要命,这个等待短则五分钟,多则一个小时。我会想,有没有搞错,Windows 的产品经理(按惯例姑且认定这些特性的设计是产品经理干的吧)是怎么想的?这样的荒唐功能居然能发布出来 ?
首先,系统更新升级这个事儿是必要的,并且对系统资源的显著消耗在很多情况下是不可避免的。但是,通常情况下,不能把更新升级这件事,变成一件阻碍用户使用的事情。
阻碍有三种级别:
- 一种是引导用户,用户感知性不大,这是比较理想的情况,用户在某种引导下使用,但并不明显感到阻碍本身。
- 第二种是还能使用,但是感到明显阻碍,比如弹窗之类的情况。
- 第三种就是彻底不能用,开机更新就是如此。
关于系统更新,来考虑这么几种情况:
- 关机时更新;
- 用户使用时在后台更新;
- 开机时更新;
- 半夜里自动更新。
你看,关机时更新可能相对比较好接受一点,虽然也有例外,但毕竟,多数时候关机就意味着用户不想使用了,这时候占用一些资源和用户的时间去更新,用户不太容易抱怨。
后台更新这个比较敏感,如果用户在做事情,CPU 或者磁盘占用飚到 100%,这绝对是要命的糟糕体验,遗憾的是这在 Windows 简直是常态,我已经不记得多少次用着电脑的过程中,突然卡得不像样,勉强调出任务管理器,看到的都是 Windows 那些乱七八糟的服务在努力工作,把所有资源都占了 。
开机时更新,可能是最糟糕选择。用户开机,就是想使用电脑,对于阻碍用户,并且是长时间阻碍用户做事情的特性,应该第一优先被砍掉。
半夜里自动更新,这个也有争议,毕竟 Windows 糟糕的设计太多,一旦自动唤醒的功能打开,半夜里 Windows 不断被唤醒,鼠标能唤醒,键盘也能唤醒,歇不了 5 分钟就唤醒,唤醒和休眠的噪音实在是很折磨人。
我认为,这几个选项相对来说还是半夜里自动更新更好,只要被反复频繁唤醒的问题能够解决,其次是关机时更新。当这样的特性拿不准的时候,也可以在第一次需要更新前询问用户,即交给用户决策,像 iPhone 会询问能不能今天晚上自动更新,或者现在就更新。让用户决策也是一种打扰用户的方式,因而不是一个最佳的解决方案,然而,在不经过用户无法做出比较合理的重要决定的时候,是一个可以考虑实行的方案。另外,对于不重要的更新,完全可以等待,攒一批一起操作。
最后,Windows 系统使用方面的问题实在是太多了,这只是其中比较烦人的一个。
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》
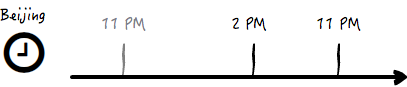
有关地图算法请教一个问题:
在分子模拟中存在这样的算法,将原子归到元胞中来快速得到其周围的信息。
对餐馆能否使用类似的思路?(计算元胞位置时 O(N),而建立原胞后检查位置
时仅取决于邻居数与元胞大小?能想到的问题是餐馆稀疏时内存占用较大。)
https://zh.wikipedia.org/wiki/%E5%85%83%E8%83%9E%E5%88%97%E8%A1%A8
有没有可能未来的操作系统不需要更新呢?
從已排序的經度中找出符合的區間 (log(n)), 再一一檢查區間內每個點 (n) 的緯度是否在上下界內, 這樣是 O(n) 。
对,我修改一下