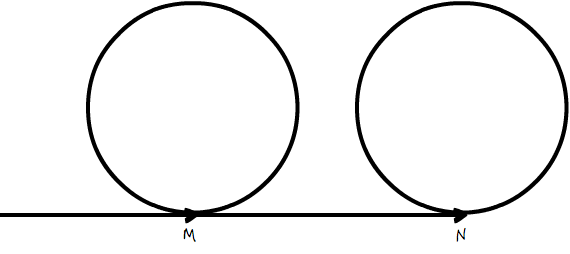
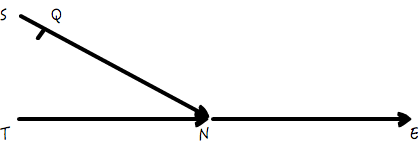
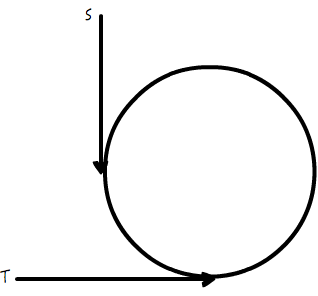有这样一个经典的算法题,说是一个单向链表,它内部可能存在环,也可能不存在,用怎样的方法,可以检测出,这个链表是否存在环。下图即是这个形成环的示意,如果单向链表的尾部,指向了链表中的一个节点,而不是指向空,那就构成环了。
接着的一个问题是,怎么检测出这个链表是否有环?
看到这个问题,也许你会觉得,太简单了,但是这个问题只是一个引子。在 《求第 K 个数的问题》一文中,我从简入深,逐步展开,把这 “第 K 个数” 的一系列问题翻了个底朝天。我想关于这个链表成环问题,我也利用类似的思路,看看我是不是也能把这一个问题前前后后讲清楚。
判断单向链表是否成环
在进一步思考怎样判断这个成环的问题以前,先考虑一件事情,如果成环,有没有可能成一个以上的环?
从图示上看,似乎说得通,可事实上却是不可能的,因为 M 点需要有两个后继节点,一个用于构成该处的环,一个用于指向 N 的方向,这显然对于一般我们说的单向链表来说,是不可能做到的。
那么,怎么检测单向链表是否成环呢?
网上能见到的最普遍的解决方法就是双指针,一快一慢,从链表头部开始,快的每次走两步,慢的一次走一步,交替进行,直到二者相遇或快指针抵达链表尾部。如果相遇说明存在环。
不过,这是一个巧妙的方法,是一个时间复杂度在 O(n)、空间复杂度在 O(1) 的好方法,却不是唯一的方法。还有一个思路是,用某种方式记录下走过的节点,如果再次遇到了,就说明成环了。这种方法只需要一个指针,且不会重复遍历走过了的节点,但缺点是存在记录走过节点的开销:
- 如果链表节点允许使用某变量标记状态(例如 visited 这样的布尔值),当然可以,且不需要额外的空间复杂度;
- 如果不允许,可以额外使用一个 HashSet 来记录节点,如果存在过,就找到节点了,这种方式的空间复杂度是 O(n)。
再回到那个一快一慢的双指针问题上,有一些基本的问题需要搞清楚。
一快一慢的双指针,在链表成环的情况下,它们一定会遇到吗,有没有可能恰好错过呢?
不会错过,一定会相遇。我们分两种情况考虑:
- 一种情况是快指针恰好落后慢指针一个身位,那么显然慢指针之后的那个位置,就是它们下一个回合碰面的位置;
- 另一种情况是快指针落后更多,那么快指针会慢慢赶上来,因为每一个回合快指针走两步,而慢指针走一步,因此每一个回合二者都可以缩短长度为 1 的距离,直到前面说到的只差一个身位的情况出现。
寻找环入口
那么,下一个自然的问题是,怎样找到那个从单向链表进入环的节点(环入口)?
乍一看这个问题,可能很难找到一个高效的解决方法。我们先退一步,仔细分析一下刚才判断成环的步骤,这里面利用了一个事实,如果链表成环,那么快慢指针一定会相遇。那么一个很自然的问题是,它们会在哪里相遇?
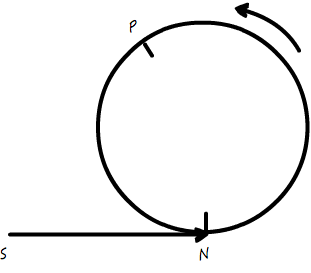
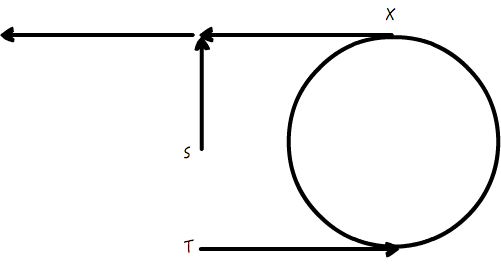
首先,它们肯定在环上相遇,因为直线部分 SN 不可能出现 “追上” 的现象。那么,假设它们相遇的点为 P:
- 对于快指针来说,从起点 S 走到 P 点,假如说绕了 m 圈,环周长为 p,那么一共走了 SN + mp + NP,其中 NP 为最后一圈从 N 逆时针走到 P 的距离。
- 而对于慢指针来说,从 S 走到 P 点,一定只绕了不到一圈,也就是一共走了 SN + NP 的距离。
这里有个问题,为什么慢指针从 S 走到 P 点,一定只绕了不到一圈?
因为对于慢指针来说,在 “运气最背” 的情况下,就是它刚抵达 N 点的时候,快指针恰好已经路过 N 了,因此在 N 没有相遇。那么按照快指针两倍于慢指针速度的情况来说,慢指针一圈之内,也就是快指针两圈之内一定可以发生 “赶上并超过”,那么也就一定会发生 “相遇”(由于前面的结论,它们不会错过)。因此,这种情况下,相遇的时候,慢指针一定还没有绕足一圈。
好,由于我们知道在 P 点相遇的时候,快指针实际走了慢指针两倍的距离,于是得到:
SN + mp +NP = 2 * (SN + NP)
所以,我们得到:
mp = SN + NP
这意味着什么?这意味着因为 SN+NP 是环周长的倍数,也就意味着在快慢指针相遇在 P 点的时候,如果这个慢指针继续走 SN 的距离,不管这个 SN 实际会绕多少圈,一定会最终停到 N 点。
我们虽然还是不知道这个 SN 有多长,但是我们在快慢指针相遇在 P 点的时候,把快指针撤回起点,并且给了快指针一个新指令——你和慢指针一样,每次走一步。这样,慢指针从 P 点开始,逆时针向 N 逼近;快指针从 S 点开始,也以同样的速率向 N 逼近。等它们相遇的时候,恰好就是 N 点,也就是环入口。同时,也获知了 SN 的长度。
计算环周长
如果环入口准确定位了,那么环周长也自然不成问题了。
从环入口开始计数,直到若干步后,重新回到环入口。知道了环周长,根据前面获知的 SN,也就知道了 NP(从环入口 N 逆时针遍历到快慢指针相遇点 P)的距离。
判断链表相交
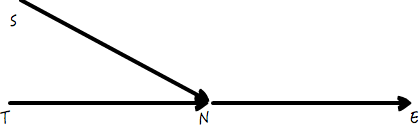
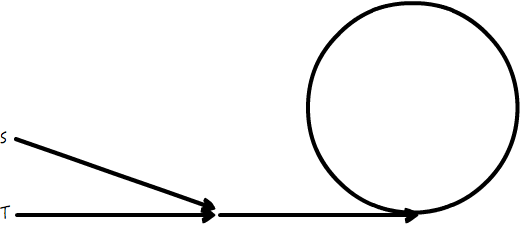
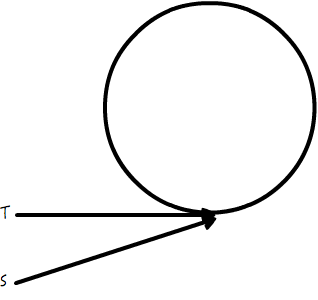
链表相交,指的是两个不同的链表,链表头不同,但是链表尾部却相同。如图所示:
其中,一个链表从头部 S 开始,另一个从头部 T 开始,二者相交在节点 N,最后共同收尾于 E。
怎样判断链表是否相交,如果是,又怎样找到相交的节点 N?
根据前面寻找环入口问题的启示,如果 SN 的长度等于 TN,那么一个指针从 S 开始,另一个从 T 开始,一样的速率前进,相交的地方就是 N。
但是 SN 和 TN 并不一定相等。
不过也没关系,先对于链表 S-N-E,遍历一遍,得到长度 l1;再对于链表 T-N-E,遍历一遍,得到长度 l2,对于二者中长度较长的一个,让这个指针单独先走一段(以下图为例,从 S 走到 Q),走的这段长度恰好为 l1 和 l2 的差值,把这段差值给抹平。这样一来,QN 就等于 TN 了,这样两个指针就可以同样速率往后前进了,相遇的 N 点就是相交的节点;如果一直不相遇,那就是没有相交。
链表相交和链表成环一起出现
都很简单是不是?有了前面的铺垫,下面来讨论最复杂的问题。
假如说,链表成环和链表相交一起出现,即分别有两个链表,它们可能成环,也可能相交,还可能既成环、又相交。现在,怎样判断它们是否成环,如果成环,环入口在哪里?是否相交,如果相交,相交点又在哪里?
看起来似乎问题一下子复杂了很多,可是仔细观察一下这两个问题,它们的地位不是均等的——
- 成环的判断,并不依赖于相交的判断。换言之,无论两个链表是否相交,都可以利用前面所述的成环判断,和环入口的计算方式求得。
- 可是相交的判断却依赖于成环的判断。换言之,要求相交的点需要知道链表的长度,而一旦链表成环了,这个长度就不再能用通用的方法来求解了。
因此,先判断链表是否成环,并且分别求出这两个链表的环入口(如果成环的话),之后再考虑链表相交的问题。
接着,关于成环和相交,我们先按照这两个链表各自是否具有环来进行如下分类:
两个链表都不成环
如果这两个链表都不成环,那么问题退化为前面讲的相交问题。这是最简单的 case。
只有一个链表成环
如果这两个链表,一个成环,而另一个不成环,那么它们二者肯定不相交。这个结论是显然的,因为相交,意味着这个环是共用的,那么自然不可能一个成环,而另一个不成环了。
可是也许你可能会说,不对,如果先成环,成环之后再出现相交呢,这样环就可以不是共用的了,于是不就可以两个链表相交,且一个链表成环,而另一个不成环了吗?
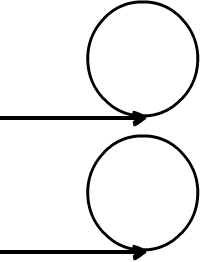
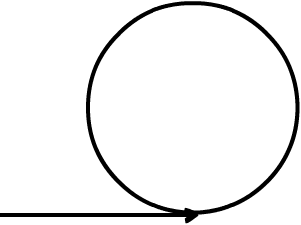
不对,这样是不行的,在相交的情况下,要成环且这个环不共用,只能出现下面这种情况:
上图中,这个环只被以 T 为头部的链表单独拥有,而不被以 S 为头部的链表所拥有。可是,这个图是错的,错的地方就在于,我们已经讨论过了,在环上是无法分叉出去的,即 X 点是不可能存在的。
两个链表都成环
这时,这个问题就比较有意思了,下面我们按照相交点出现的位置来分别讨论。
这种情况下,我们把环入口的点视作两个链表的尾部,然后可以用前面所述的算法求得相交的点。
如果在遍历到环入口以前,找到了两个链表相交的节点,那么我们遇到了情况一,相交的节点先于成环的节点出现:
反之,如果遍历到环入口时,依然没有发现相交的节点,那么存在下面所述的情况二、三和四:
情况二,成环且不相交,相当于两个独立的带环链表:
情况三,环入口和相交的节点一起出现:
情况四,属于情况三的特殊版本,两个环入口出现在同一个点:
有没有可能有情况五,即先出现环入口,再出现相交的节点?
不可能。因为前面已经介绍了,相交就意味着一旦有环,这个环就是两个链表共用的,因此这个环入口一旦出现,就意味着一个链表连上了另一个链表的环,也就意味着相交点也出现了。因此,这种情况下二者是一起出现的,不可能出现环入口早于相交节点的情况。
那么现在的问题是,怎样区分情况二、三和四?
首先检测是不是两个环的环入口共用,如果共用,就是情况四;反之,根据如下策略区分情况二还是三:
既然两个环入口都找到了,那么以任意一个环入口作为起点,开始遍历,绕环一周,如果期间遇到了另一个环入口,说明是情况三,否则则是情况二。
好,这个问题就讨论到这里。你也可以看到,如果单独拿出最后一个问题来,这是一个有着相当复杂度的问题。不过如果逐步深入进来的话,应该就好很多。
记得在差不多快要十年前了,我 “莫名其妙” 地参加了微软的面试,而电话面试问的题目就是本文一开始的链表成环判断的问题。由于对外企面试的玩法一无所知,我被虐得体无完肤。现在看起来这实在是一个太过普通的问题,但当时的我对于算法的认识是非常浅的,也没有给出一个非常好的解决办法。但是从那一天开始,我才真正算是逐步开始接触并学习算法,因此这篇文章,也算对它小小的纪念。
最后,我想说明的是,在分析上面这些问题的时候,我没有写一点代码。我觉得,这样的纯算法问题,只要思路清楚了,代码基本不是什么问题。
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》